Điều khiển mạng nơ-ron và các ứng dụng của điều khiển mạng nơ-ron
1. Mạng nơron nhân tạo (Neural network)
1.1 Định nghĩa
- Mạng nơron là sự tái tạo bằng kỹ thuật những chức năng của hệ thần kinh con người. Mạng nơron gồm vô số các nơron liên kết với nhau.
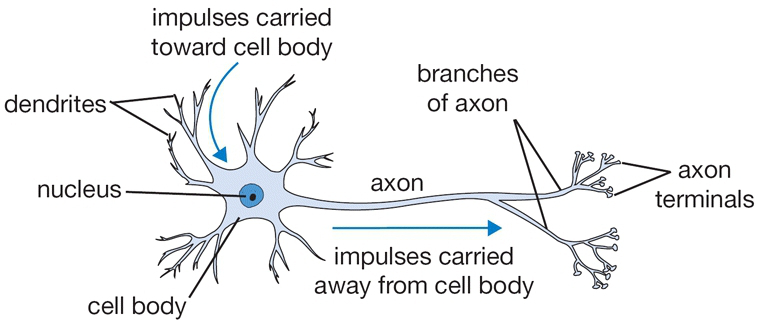
Mạng nơ-ron nhân tạo
1.2 Đặc tính
Hai đặc tính cơ bản của mạng nơron là:
+ Quá trình tính toán được tiến hành song song và phân tán trên nhiều nơron gần như đồng thời.
+ Tính toán thực chất là quá trình học, chứ không phải theo sơ đồ định sẵn từ trước.
1.3 Mô hình toán
Mô hình toán của mạng nơron nhân tạo: (Artifical Neural Networks)
Đây là mô hình điều khiển dạng MISO, với đầu vào là n tính hiệu X={x1,x2,…xn }T, đầu ra là tín hiệu y được xác định:
y(t) = q**wk*{x1,x2,…xn }T/f
trong đó q là ngưỡng kích hoạt nơron, wk là các trọng số, f là hàm kích hoạt.
1.4. Cấu trúc mạng nơron
Nguyên lý cấu tạo của một mạng nơron là bao gồm nhiều lớp, mỗi lớp bao gồm nhiều nơron có cùng một chức năng.
Sau đây là các dạng liên kết mạng cơ bản:
a) Mạng truyền thẳng (Feedforward Neural Networks)
b) Mạng có hồi tiếp
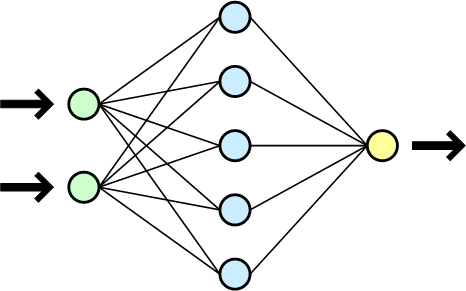
Mạng nơ-ron nhân tạo
1.5 Một số mạng nơron cơ bản
- Mạng MLP (Multilayer perceptron)
Có rất nhiều công trình nghiên cứu về mạng MLP và đã cho thấy nhiều ưu điểm của mạng này. Mạng MLP là cơ sở cho thuật toán lan truyền ngược và khả năng xấp xỉ liên tục.
Thuật toán lan truyền ngược:
Tập dữ liệu đã cho có n mẫu (xn,dn), với mỗi n, xn là tín hiệu đầu vào, dn là đầu ra mong muốn. Quá trình học là việc thực hiện cực tiểu hoá hàm G sau:
G = Gn, với Gn =a,x
Q là số nút tại lớp ra của mạng. Còn trọng số liên kết mạng được điều chỉnh theo phép lặp, trong đó m >0 là hằng số tỷ lệ học.
Mạng MLP là một giải pháp hữu hiệu cho việc mô hình hoá, đặc biệt với quá trình phức tạp hoặc cơ chế chưa rõ ràng. Nó không đòi hỏi phải biết trước dạng hoặc tham số.
- Mạng RBF (Radial basis functions)
Biểu diễn toán học của RBF
trong đó C : véctơ chứa trọng số RBF
R : véctơ chứa các tâm RBF
j : hàm cơ sở hoặc hàm kích hoạt của mạng
F(x) : hàm nhận được từ đầu ra của mạng
C0 : hệ số chệch
|| || : chuẩn Euclide
Nhờ khả năng xấp xỉ các hàm phi tuyến bất kì với độ chính xác tuỳ ý, mạng nơron, đặc biệt là mạng RBF là công cụ quan trọng cho mô hình hoá hệ thống và cho điều khiển thích nghi các hệ thống phi tuyến.
2. Nhận dạng mô hình và điều khiển sử dụng mạng nơron
2.1. Nhận dạng thông số mô hình
Nhận dạng thông số chính là quá trình luyện mạng. Tín hiệu sai số là cơ sở cho luyện mạng, D là thời gian trễ.
2.2. Điều khiển sử dụng mạng nơron
Ta có nhiều cấu trúc điều khiển sử dụng mạng nơron như:
- Điều khiển theo vòng hở
- Điều khiển theo vòng kín
- Điều khiển với mô hình tham chiếu
- Điều khiển theo thời gian vượt quá (over time)
- Bộ điều khiển với quyết định hổ trợ của mạng nơron
3. Ứng dụng điều khiển mạng nơ-ron nhân tạo
Mạng nơ-ron nhận tạo được ứng dụng trong nhiều lĩnh vực của đời sống xã hội. Chủ yếu là trong: điện, điện tử, quân sự, kinh tế…Nhờ có Neural network mà những bài toán cao cấp, có độ khó phức tạp cần độ chính xác cao và gần như tuyệt đối đó là:
- Nhận dạng hệ thống
- Điều khiển tự động
- Khai phá dữ kiệu
Người ta đã chứng minh rằng một mạng tiến với các hàm kích hoạt phi tuyến, liên tục và khả vi có khả năng xấp xỉ phổ quát. Các mạng hồi quy cũng đã được sử dụng để nhận dạng hệ thống. Nhất định, một tập các cặp dữ liệu đầu vào - đầu ra, nhận dạng hệ thống nhằm mục đích hình thành một ánh xạ giữa các cặp dữ liệu. Một mạng lưới như vậy được cho là sẽ nắm bắt được động học của một hệ thống.
3.1 Một số ứng dụng mạng nơ-ron trong điều khiển:
- Điều khiển theo vòng hở
- Điều khiển theo vòng kín
- Điều khiển với mô hình chuẩn
- Mô hình điều khiển dự báo
- Phản hồi tuyến tính hóa thích nghi dùng mạng nơ-ron
- Bộ điều khiển với quyết định hỗ trợ của mạng nơ-ron
3.2 Một số ví dụ ứng dụng mạng nơ-ron trong điều khiển:
- Điều khiển cánh tay máy theo mô hình chuẩn

Điều khiển cánh tay theo mô hình chuẩn
- Điều khiển dự báo hệ bồn phản ứng dùng mô hình mạng nơron
- Điều khiển tốc độ động cơ điện một chiều
- Để điều khiển thiết bị bằng giọng nói
- Để dự báo mưa và dòng chảy trong công tác phòng tránh và giảm nhẹ thiên tai
- Neural network trong công cuộc xử lý tín hiệu bị nhiễu
- Mạng nơ – ron biến hình phẳng thành mô hình 3D
- Neural network trong công tác nhận diện giọng nói của các thiết bị điện tử
- Neural network cho các ứng dụng dịch ngôn ngữ
- Chắc chắn sẽ không làm bạn thất vọng
- Liên hệ để được hỗ trợ chi tiết: 0936.985.256












